Noi conosciamo persone che hanno frequentato per anni le scuole di filosofia senza prendere neanche un po' di ..... tintarella.
Seneca Lettere morali a Lucilio
Può il battito d'ali di una farfalla scatenare un uragano a migliaia di chilometri di distanza? Quando Edward Lorenz, meteoreologo del Massachusetts Institute of Technology di Boston (MIT), pose questa domanda ai colleghi che erano presenti a un congresso, questi restarono allibiti. Lorenz aveva scoperto un fatto nuovo: partendo da due stati iniziali anche solo leggermente differenti, un sistema può seguire evoluzioni molto diverse. Nel corso di un programma di simulazione del clima, Lorenz aveva fatto
un'inaspettata quanto importante scoperta. Una delle simulazioni climatiche si basava
su dodici variabili, incluse relazioni non lineari. Lorenz scoprì che, ripetendo la stessa
simulazione con valori iniziali leggermente diversi l'evoluzione del clima
elaborata dal computer si discostava nettamente dai risultati precedenti: a quella che
si configurava appena una perturbazione, dopo un'effimera somiglianza iniziale, si
sostituiva un modello climatico completamente diverso.
Queste osservazioni hanno portato allo sviluppo della Teoria del Caos che pone
limiti alla prevedibilità dell'evoluzione di sistemi complessi non lineari. Nei
sistemi lineari, una piccola variazione nello stato iniziale di un sistema fisico,
chimico, biologico, o economico provoca una variazione corrispondentemente
piccola nel suo stato finale: per esempio, colpendo leggermente più forte una palla da
biliardo, questa andrà più lontano.
Al contrario, sono non lineari le situazioni di un sistema in cui piccole
differenze nelle condizioni iniziali producono differenze non prevedibili nel
comportamento successivo. Un sistema può anche comportarsi in modo caotico in
certi casi e in modo non caotico in altri. Per esempio, da un rubinetto non chiuso le gocce cadono in una sequenza
regolare, variando leggermente l'apertura del rubinetto, si può far sì che le gocce
cadano invece in modo irregolare, appunto caotico. E' impossibile prevedere il
comportamento che un sistema caotico avrà dopo un intervallo di tempo anche
piuttosto breve. Infatti, per calcolare il comportamento futuro del sistema, anche se
descritto da un'equazione molto semplice, è necessario inserire i valori delle
condizioni iniziali.
D'altra parte, nel caso di un sistema complesso non lineare, data la grande
sensibilità del sistema agli agenti che lo sollecitano, un piccolo errore nella misura
delle condizioni iniziali, oppure una modifica apparentemente irrilevante dei dati
immessi ed ovviamente anche il loro successivo arrotondamento durante il calcolo,
cresce esponenzialmente con il tempo, producendo un radicale cambiamento dei
risultati.
Questo significa che i dati relativi alle condizioni iniziali dovrebbero essere
misurati con un'accuratezza teoricamente infinita, ma ciò é praticamente impossibile.
Quanto detto spiega perché le previsioni meteorologiche, sebbene descritte con le
equazioni deterministiche della fisica, fluidodinamica e termodinamica, ed elaborate
con raffinate tecniche di calcolo eseguite da super computer, producono risultati
molto approssimativi. I processi atmosferici, d'altra parte, sono estremamente vari e
complessi, in quanto comprendono fenomeni limitati e di breve durata come
temporali e trombe d'aria, e fenomeni estesi per migliaia di chilometri come i sistemi
monsonici, stabili per alcuni giorni o mesi.
Per rappresentare l'atmosfera sono necessari sei milioni di numeri e questo
comporta i problemi connessi alle misurazioni. Gli strumenti a terra sono molto
accurati, ma le sonde in quota possono rilevare la temperatura con un errore di un
grado; i satelliti pagano lo scotto di sondare spazi altrimenti irraggiungibili con errori
anche di due gradi.
L'effetto farfalla, in conclusione, sottolinea come nella maggior parte dei
sistemi biologici, chimici, fisici, economici e sociali, esistano degli elementi che,
apparentemente insignificanti, sono in grado, interagendo fra loro, di propagarsi e
amplificarsi provocando effetti catastrofici. Questi elementi, e perché trascurati, e
perché imprevedibili, e perché non individuabili, costituiscono il dilemma del nostro
secolo giacché, come abbiamo visto, possono condurci a conclusioni errate. Ecco il
motivo per cui molto spesso, ad esempio, per spiegare il comportamento di un
sistema come la crescita della popolazione, l'eutrofizzazione delle coste marine, o le
variazioni climatiche, si ricorre a un modello.
Un modello è una riproduzione semplificata della realtà, ossia un'astrazione
che considera solamente le principali caratteristiche di quello che è il reale oggetto di
studio. Tuttavia, un modello, sebbene possa sembrare limitato, in quanto non
riproduce completamente la realtà, permette di esaminare gli aspetti piú importanti di
un problema.
E non è poco: se considerassimo tutti i dettagli di un problema, ottenendo
quello che si definisce una simulazione come quella meteorologica, ci troveremmo ad
affrontare un insieme di dati difficilmente correlabili tra loro e quindi la loro analisi
ci sarebbe impossibile o di utilità limitata all'analisi di brevi periodi, come appunto
per le simulazioni climatiche.
Certo, come abbiamo visto, un modello non può offrire garanzie di sicurezza
assoluta ma è comunque un indispensabile strumento per il progresso della scienza e
della tecnologia. Per convincersene, basta pensare che l'uso di un modello è del tutto
naturale. Ad esempio, quando usciamo da casa per recarci al lavoro o per una gita, ci
formiamo mentalmente l'idea del percorso che seguiremo, con la sosta per il giornale,
o per il caffè, ma certo non prenderemo in considerazione la possibilità che un condor
atterri sul tetto della nostra auto o altri eventi improbabili. Automaticamente il
pensiero opera una semplificazione della realtà per poter elaborare delle conclusioni
su di lei.
A ben guardare poi, il Caos, ci circonda più di quanto immaginiamo. Il cervello umano è composto da un
numero enorme di elementi semplici, i neuroni, che scambiano tra loro impulsi elettrici. Tuttavia questo sistema è capace di percepire sensazioni e formare pensieri. Il cervello è dunque ciò che la fisica definisce "Sistema Complesso'', anzi è il miglior esempio di tale sistema, difficilmente prevedibile e quindi caotico.

Il fumo di un fiammifero, esempio di sistema caotico
Eppure anche il Caos ha le sue regole e scoprirle attraverso quella che è stata definita la Scienza del Caos "consentirebbe di fare previsioni sempre più affidabili risalendo attraverso la catena delle cause e degli effetti fino "all'effetto farfalla''.
Nella realtà, l'espressione "Effetto farfalla'' si ritiene sia stata ispirata da uno dei più celebri racconti fantascientifici di Ray Bradbury: Rumore di tuono (A Sound of Thunder) del 1952, in cui si immagina che nel futuro, grazie ad una macchina del tempo, vengano organizzati dei safari temporali per turisti. In una remota epoca preistorica un escursionista del futuro calpesta una farfalla e questo fatto provoca una catena di allucinanti conseguenze per la storia umana.
E quello,- disse - è il Sentiero che la Time Safari ha preparato
per voi. è di metallo antigravità, e sta sospeso a venti centimetri
da terra, senza toccare nè un fiore nè un albero nè un solo filo d'erba.
Il suo scopo è di impedirvi di toccare in qualsiasi modo questo mondo
del passato. (...) Gestire una macchina del tempo è una faccenda complicata.
Uccidendo un animale, un uccellino, uno scarafaggio o anche un fiore,
potremmo senza saperlo distruggere una fase importante di una specie
in via di evoluzione. (...) Supponiamo di uccidere un topolino qui.
Ciò significa che tutte le future famiglie di questo particolare topolino
non potrebbero più esistere (...). Per ogni dieci topolini che non
ci sono, muore una volpe. Se mancano dieci volpi, un leone muore di
fame. Se manca un leone, innumerevoli insetti, avvoltoi, quantità
infinite di forme di vita piombano nel Caos e nella distruzione. (...) A Sound of Thunder. (Traduzione di Stefano Negrini, Editori Riuniti, 1985)
Alan Turing in un saggio del 1950, Macchine calcolatrici ed intelligenza, anticipava questo concetto: lo spostamento di un singolo elettrone per un miliardesimo di centimetro, a un momento dato, potrebbe significare la differenza tra due avvenimenti molto diversi, come l'uccisione di un uomo un anno dopo, a causa di una valanga, o la sua salvezza.
Per esemplificare con un'idea concreta e quotidiana questo concetto, si parla solitamente delle cosiddette "porte scorrevoli'': una persona deve assolutamente prendere il treno, ma ritarda di giusto due secondi e lo perde. Perdendolo, entra in scena una sequenza di avvenimenti che la porta, ipotizziamo, a ritornare a casa deluso ed imbattersi casualmente nella donna della propria vita svoltando distrattamente l'angolo. Se invece la persona fosse riuscita a prendere il treno, si sarebbe trovata da tutt'altra parte e non avrebbe conosciuto quella donna.
A conti fatti perciò una singola azione può determinare imprevedibilmente il futuro - nella metafora della farfalla, quindi, si immagina che un semplice movimento di molecole d'aria generato dal battito d'ali di una farfalla possa causare una catena di movimenti di altre molecole fino all'uragano menzionato. Così un semplice ritardo di due secondi può incidere sulla vita personale di un individuo. Ovviamente qualsiasi evoluzione degli eventi nei due casi è ipotizzabile e plausibile: e se magari fermando la propria anima gemella le avesse impedito di essere investita da un camion pochi metri dopo? E se prendendo il treno invece avesse per sbaglio preso al capolinea una valigia, uguale alla propria, di un'altra persona contenente esplosivo a tempo, sventando così un attentato a prezzo della propria vita?b
Edward Lorenz fu il primo ad analizzare l'effetto farfalla in uno scritto del 1963 preparato per la New York Academy of Sciences. Secondo tale documento, "Un meteorologo fece notare che se le teorie erano corrette, un battito delle ali di un gabbiano sarebbe stato sufficiente ad alterare il corso del clima per sempre.'' In discorsi e scritti successivi, Lorenz usò la più poetica farfalla, forse ispirato dal diagramma generato dagli attrattori di Lorenz, che somigliano proprio a tale insetto, o forse influenzato dai precedenti letterari (anche se mancano prove a supporto). "Può il batter d'ali di una farfalla in Brasile provocare un tornado in Texas?'' fu il titolo di una conferenza tenuta da Lorenz nel 1979.
La meccanica classica è deterministica. Governa il movimento dei pianeti e dei satelliti. Le sue leggi furono stabilite da Galileo e Newton e sviluppate tra il XVII e il XIX secolo da fisici e matematici. Conosciute le forze che agiscono su un corpo, e data la sua posizione e la sua velocità iniziali, la meccanica classica permette di calcolare la traiettoria del corpo. Questo è il determinismo.
Il determinismo assoluto in fisica cominciò a essere contestato alla fine del XIX secolo da alcuni teorici, come Ludwig Boltzmann, che introdussero il concetto di probabilità per dare un'interpretazione meccanica alla termodinamica. La descrizione globale di un gas in un contenitore non dipende dal comportamento delle singole molecole ma dipende dalle medie statistiche su una grande massa di molecole. Qui subentra la teoria della probabilità.
Il determinismo subì una revisione ancora più profonda con l'avvento della meccanica quantistica e, in particolare, del principio di indeterminazione di Heisenberg che mostrò come il concetto di traettoria non avesse senso nella meccanica quantistica.
Il primo che intravide la possibilità che anche la meccanica classica potesse non essere tanto deterministica fu il fisico francese Henri Poincaré.
Poincaré anticipava i tempi e in un’epoca ferocemente determinista cominciava a vedere i limiti della prevedibilità matematica del mondo meccanico e infatti aveva una risposta a quell’interrogativo: «Le grandi perturbazioni – scrive Poincaré – si producono in genere nelle regioni in cui l’atmosfera è in equilibrio instabile. I meteorologi vedono bene che quest’equilibrio è instabile, che un ciclone sta per nascere da qualche parte; ma dove non sono in grado di dirlo; un decimo di grado in più o in meno in un punto qualunque e il ciclone scoppia qui e non là e stende le sue devastazioni su contrade che avrebbe risparmiato. Se si fosse conosciuto questo decimo di grado, lo si sarebbe potuto sapere in anticipo, ma le osservazioni non erano né abbastanza ravvicinate, né abbastanza precise, ed è per questo che tutto sembra dovuto all’intervento del caso. Qui troviamo ancora lo stesso contrasto tra una causa minima, inapprezzabile per l’osservatore, e degli effetti considerevoli, che sono a volte degli spaventosi disastri».
Inoltre nel corso dei suoi studi sul problema dei tre corpi soggetti a reciproche gravità, Poincaré scoprì che esistevano situazioni nelle quali non era possibile dare una sola soluzione alle traettorie dei tre corpi.
Con un approccio scientifico si afferma che la teoria del caos è lo studio attraverso modelli della fisica matematica dei sistemi fisici che esibiscono una sensibilità esponenziale rispetto alle condizioni iniziali. I sistemi di questo tipo sono governati da leggi deterministiche, eppure sono in grado di esibire una empirica casualità nell'evoluzione delle variabili dinamiche. Questo comportamento casuale è solo apparente, dato che si manifesta nel momento in cui si confronta l'andamento temporale asintotico di due sistemi con configurazioni iniziali arbitrariamente simili tra loro.
Comunque non fu prima della metà del XX secolo che quello che oggi conosciamo con l'ossimoro di "caos deterministico" fece la sua irruzione definitiva. E lo fece quasi simultaneamente in varie discipline: i computer potevano infatti affrontare problemi che i metodi tradizionalu non erano riusciti a risolvere.
Il caos deterministico si presenta, quando un corpo soggetto a regole determinate si comporta in modo irregolare e apparentemente casuale. Esso si discosta,. però, da un comportamento puramente casuale e la sua caratteristica principale è la sensibilità alle condizioni iniziali: due stati molto vicini possono dar luogo a futuri molto diversi.
La nascita vera e propria di questa teoria scientifica si verifica però nel 1963, quando Edward Lorenz pubblica il suo articolo Deterministic Nonperiodic Flow, nel quale tratta del comportamento caotico in un sistema semplice e deterministico, con la formazione di un strattrattoreano.
Negli anni successivi numerose scoperte in questo ambito fatte da Mitchell J. Feigenbaum, che scoprì l'universalità di alcune costanti a partire da uno studio sull'applicazione logistica, lo portarono a una teoria sullo sviluppo della turbolenza nei fluidi. Il matematico belga David Ruelle e il fisico olandese Floris Takens furono i pionieri della teoria degli attrattori strani.
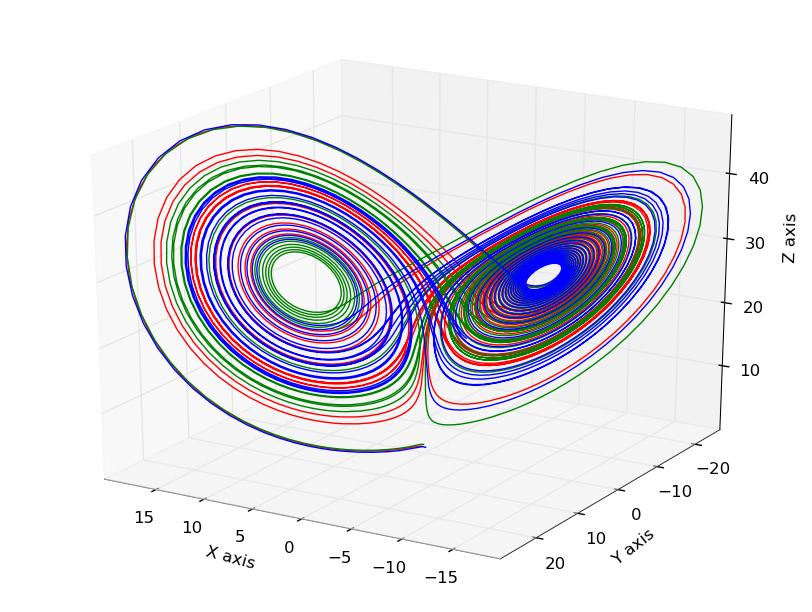
Attrattore strano do Lorentz
In matematica, un attrattore è un insieme verso il quale evolve un sistema dinamico dopo un tempo sufficientemente lungo. Perché tale insieme possa essere definito attrattore, le traiettorie che arrivano a essere sufficientemente vicine ad esso devono rimanere vicine anche se leggermente perturbate. Dal punto di vista geometrico un attrattore può essere un punto, una curva, una varietà (varietà stabile), o anche un insieme più complicato dotato di struttura frattale e noto con il nome di attrattore strano (Un frattale è un oggetto geometrico dotato di omotetia interna: si ripete nella sua forma allo stesso modo su scale diverse, e dunque ingrandendo una qualunque sua parte si ottiene una figura simile all'originale. La natura produce molti esempi di forme molto simili ai frattali. Ad esempio in un albero (soprattutto nell'abete) ogni ramo è approssimativamente simile all'intero albero e ogni rametto è a sua volta simile al proprio ramo, e così vi). Una traiettoria di un sistema dinamico su un attrattore non deve soddisfare nessuna proprietà particolare, escludendo il fatto che deve rimanere sull'attrattore. Le traiettorie possono essere periodiche, caotiche o di qualunque altro tipo.
Dalla scoperta di Lorenz molto cammino è stato compiuto in tutte le branche
del sapere. Tra tutte le definizioni che si possono dare sul 1900, una sembra la più significativa: il
1900 è il secolo delle Rivoluzioni. Dopo la Relatività e la Meccanica Quantistica, la
rivoluzione più importante è la scoperta della teoria del Caos.
Essa ha investito spazi come quello dei matematici, dei fisici, dagli studiosi della meccanica dei liquidi, agli
astronomi, dei chimici e degli studiosi di etologia, degli informatici e di quanti si
occupano di crittografia, dei cardiologi, degli analisti, dei chirurghi, degli studiosi del
comportamento nell'organizzazione aziendale, nella comunicazione o nella geriatria.
In tutte le discipline lo studio del Caos ha dato conferme sorprendenti e
sorprendenti ne sono state finora le conseguenze applicative. Gli studi di tutti gli
scienziati dimostrano che il comportamento naturale dei fenomeni è non lineare, anzi
che la vita stessa è possibile perché c'è il caos.
I comportamenti della maggioranza dei fenomeni della
natura e dell'uomo non procedono con ritmi che si ripetono, ma, dopo un periodo
regolare, presentano in modo inaspettato una biforcazione in un punto critico che si
moltiplica fino a generare una turbolenza. Un flusso regolare si scompone in vortici e
mulinelli. Strutture irregolari interrompono la continuità del confine tra fluido e
solido, per esempio quando il liquido si ghiaccia.
La turbolenza genera: mescolanza, disordine, causalità. Tuttavia, le
parti scomposte, i vortici nel moto dei fluidi, non fuggono via, ma restano vicini, pur
seguendo regole proprie.
Ciò avviene per un fenomeno che dà luogo ai cosiddetti attrattori strani. Esso
mescola ordine e disordine, rendendo, pur nella complessità, misurabile l'entropia.
Dunque la turbolenza si produce restando all'interno di una fase. Gli studiosi si sono
occupati di tale questione, non solo per interessi matematici o speculativi, ma per
risolvere problemi concreti, come la cura delle cardiopatie gravi, aritmie, o la stabilità
del volo degli aerei.
Alla fine dell'intero processo si produce un'autoorganizzazione in una
situazione nuova, che a sua volta può riprodurre un altro momento caotico e così via.
Ciò, come abbiamo già detto, è impredicibile, sebbene si sappia che avviene in forma
rigorosa e deterministica. Lo sviluppo così veloce dei computer che consentono
migliaia e migliaia di calcoli fa ogni giorno progredire lo studio di tale materia.
Nella vita della natura pochi sono i fenomeni lineari, mentre quelli caotici
dominano. Caotiche sono le nuvole, i fiocchi di neve e le cascate, sono caotici i
liquidi nella loro dinamica, dunque è caotico il movimento del cuore, che è la pompa
di un liquido, il sangue, contrariamente a quanto si pensava, un cuore sano ha ritmo
caotico, mentre in un cuore malato il ritmo appare sempre più regolare. La salute è caotica, la malattia è lineare. Il
Caos agisce, come si può ben constatare, nel campo dell'economia: i crolli delle
Borse sono fenomeni caotici.
Nell'uso comune, "caos" significa "uno stato di disordine". Tuttavia, nella teoria del caos, il termine viene definito con maggiore precisione. Anche se non esiste una definizione matematica universalmente accettata di caos, una definizione comunemente utilizzata afferma che un sistema dinamico deve avere le seguenti caratteristiche per essere classificato come caotico:
1.deve essere sensibile alle condizioni iniziali;
2.deve esibire la transitività topologica;
3.deve avere un insieme denso di orbite periodiche.
Dipendenza sensibile dalle condizioni iniziali
Dipendenza sensibile dalle condizioni iniziali significa che in un sistema caotico a variazioni infinitesime delle condizioni iniziali corrispondono variazioni significative del comportamento futuro. In altre parole, ogni configurazione di un sistema caotico è arbitrariamente vicina a un'altra con una traiettoria futura completamente diversa.
La sensibilità alle condizioni iniziali è comunemente nota come "effetto farfalla", effetto così chiamato per via del titolo di una relazione presentata da Edward Lorenz nel 1972 all'Associazione Americana per l'Avanzamento della Scienza a Washington, DC, dal titolo La prevedibilità: Il battere delle ali di una farfalla in Brasile provoca un tornado in Texas?. Il movimento delle ali di una farfalla rappresenta un piccolo cambiamento nella condizione iniziale del sistema, che provoca una catena di eventi che portano a fenomeni di scala sempre più vasta. Se la farfalla non avesse sbattuto le ali, la traiettoria del sistema sarebbe stata molto diversa.
È stato dimostrato che in alcuni casi le ultime due proprietà elencate sopra effettivamente implicano sensibilità alle condizioni iniziali, e se l'attenzione è limitata a intervalli, la seconda proprietà implica le altre due (una alternativa, e in generale più debole, definizione di caos utilizza solo le prime due proprietà in lista sopra). È interessante notare che la proprietà con conseguenze pratiche più significative, la sensibilità alle condizioni iniziali, è ridondante nella definizione, poiché implicita da due (o per gli intervalli, una) proprietà puramente topologica, che sono quindi di maggiore interesse per i matematici.
Una conseguenza della sensibilità alle condizioni iniziali è che se si parte con soltanto una quantità limitata di informazioni sullo stato del sistema, come avviene di solito in pratica, allora il futuro del sistema non sarà più prevedibile oltre un certo tempo. Questo è familiare nel caso del meteo, che è in genere prevedibile solo circa una settimana in anticipo. Naturalmente questo non significa che non possiamo dire nulla su eventi lontani nel futuro; ci sono alcune restrizioni sul sistema. Con tempo meteorologico, sappiamo che la temperatura non potrà mai raggiungere i 100 gradi Celsius o scendere a -130 gradi Celsius sulla Terra e che oscilla con le stagioni, ma non siamo in grado di prevedere esattamente in quale giorno avremo la temperatura più calda dell'anno. Una caratteristica peculiare di un sistema caotico, sebbene deterministico, è quindi l'apparente impredicibilità delle traiettorie del sistema, dovuta alla forte sensibilità rispetto alle condizioni iniziali.
In termini più matematici, l'esponente di Lyapunov misura il grado di sensibilità alle condizioni iniziali. Date due traiettorie di partenza nello spazio delle fasi infinitamente vicine con separazione iniziale delta Z0 queste divergono nel futuro secondo la relazione:

dove t è il tempo e lambda è l'esponente di Lyapunov. La velocità di separazione dipende dall'orientamento del vettore separazione iniziale, per cui vi è un intero spettro di esponenti di Lyapunov. Il numero di esponenti di Lyapunov è uguale al numero di dimensioni dello spazio delle fasi, anche se è comune riferirsi solo per il più grande. Per esempio, l'esponente di Lyapunov massimo è più spesso utilizzato perché determina la prevedibilità complessiva del sistema. Un esponente di Lyapunov massimo positivo è generalmente considerato come un'indicazione che il sistema è caotico.
Transitività topologica
La transitività topologica è una proprietà che implica che il sistema evolverà nel tempo in modo che ogni data regione o insieme aperto nel suo spazio delle fasi si sovrapporrà con qualsiasi altra regione data. Questo concetto matematico di "mescolamento" corrisponde all'intuizione comune fornita ad esempio dalla dinamica caotica della miscela di due fluidi colorati.
La transitività topologica è spesso omessa dalle presentazioni divulgative della teoria del caos, che definiscono il caos con la sola sensibilità alle condizioni iniziali. Tuttavia, la dipendenza sensibile dalle condizioni iniziali da sola non dà il caos. Per controesempio, consideriamo il semplice sistema dinamico prodotto da raddoppiare ripetutamente un valore iniziale. Questo sistema ha la dipendenza sensibile dalle condizioni iniziali ovunque, dal momento che qualsiasi coppia di punti vicini alla fine diventerà ampiamente separata. Tuttavia, questo esempio non ha la transitività topologica e quindi non è caotico. Infatti, ha un comportamento estremamente semplice: tutti i punti tranne 0 tenderanno a infinito positivo o negativo.
Densità delle orbite periodiche
Affinché un sistema caotico abbia un insieme denso di orbite periodiche, ogni punto nello spazio deve essere arbitrariamente vicino a una orbita periodica. La mappa logistica unidimensionale definita da x tendente a 4x(1-x) è uno dei più semplici sistemi con un insieme denso di orbite periodiche. Ad esempio, 5-5^1/2/8 tende a 5+5^1/2/8 tende a 5-5^1/2/8 (pari a circa 0.3454915 yende a 0.9045085 tende a 0.3454915) è una orbita instabile di periodo di 2, ed esistono orbite simili per periodi di 4, 8, 16, ecc.
Attrattore strano
Consideriamo un pendolo che oscilli nell’aria: il suo moto si smorza progressivamente, con oscillazioni sempre più piccole, fino a esaurirsi. L’orbita di fase è una spirale che termina nel punto velocità=0, spostamento=0, che è il punto di equilibrio del pendolo. Tutte le orbite finiscono in questo punto; esso è dunque l’attrattore del sistema.
Non tutti gli attrattori sono costituiti da semplici punti; possiamo avere delle curve regolari, dette cicli limite, oppure, nel caso dei sistemi caotici, delle strutture ancor più insolite detti attrattori strani.
Qualche sistema dinamico, come la mappa logistica monodimensionale definita da 4x(1-x) , mostra comportamenti caotici che si estendono in tutto spazio delle configurazioni, tuttavia è possibile che l'andamento caotico sia confinato solo in certe regioni di esso. Il caso di maggior interesse sorge quando un largo insieme delle configurazioni iniziali tende a convergere in una delimitata regione di spazio, l'attrattore, dove avvengono fenomeni caotici.
La regione di spazio delimitata dall'attrattore può avere dimensione intera, ma sorprendentemente questa non è l'unica possibilità. L'attrattore strano è un attrattore con dimensione di Hausdorff non intera. La dimensione degli attrattori è difficile da calcolare analiticamente e spesso viene stimata con simulazioni al computer.
Un modo semplice per visualizzare un attrattore caotico consiste nel partire con un punto nel bacino di attrazione dell'attrattore e quindi seguire la conseguente traiettoria. Dato che è valida la condizione di transitività topologica, questo equivale a produrre una immagine dell'intero attrattore finale. Un esempio famoso di questo attrattore è quello di Lorenz, la sua forma somiglia a quella di una farfalla.
Al contrario dei punti fissi, cioè attrattori monodimensionali, e dei cicli limite, con due dimensioni o più, gli attrattori che emergono dai sistemi caotici sono ricchi di dettagli e complessità e somigliano spesso a dei frattali. Strutture frattaliche possono emergere anche considerando la forma e il bordo di un bacino di attrazione di un attrattore, come ad esempio l'insieme di Julia.

Attrattore starno descritto dalla formula Xn+1 = sen (aYn) - cos (bXn)
Transizione al caos
Esistono due tipi principali di transizioni in cui i sistemi dinamici passano da un comportamento regolare a un comportamento caotico:
Transizione al caos per raddoppiamento di periodo (es. Mappa Logistica) nel quale abbiamo una transizione al caos dovuta al raddoppiamento del periodo del ciclo limite che viene creato da una Biforcazione di Hopf iniziale. In questo caso (Feigenbaum 1978) succede che dal punto fisso stabile nasce un'orbita stabile di periodo 2 (ciclo limite). Quando quest'orbita di periodo 2 diventa instabile da essa nasce un'orbita di periodo 4 e così via. La successione dei valori del parametro di controllo del sistema nei quali i diversi cicli limite così creati passano da stabili a instabili ha punto di accumulazione e tale punto di accumulazione è il punto in cui il sistema transisce al caos.
Transizione al caos per intermittenza nel quale si ha che superato il valore critico del parametro del controllo del sistema si ha ancora un comportamento regolare del sistema intervallato però da dei burst caotici. La durata di questi burst caotici aumenta all'aumentare del valore del parametro di controllo del sistema. Di questa transizione esistono 3 sottocategorie: biforcazione a nodo sella, biforcazione di Hopf inversa e period doubling inverso.
Eugenio Caruso - 20 maggio 2016

IMPRESA OGGI
Tratto da